Sets : Basic Concepts

Basic Concepts

* Any collection of well defined objects is called a set.
   

* A set may be described by listing all its members and then putting curly brackets or braces { }. This is called roster or tabular form.

* A set may be described as {x|x has property p}. This is called rule method or set builder form.

*  An infinite set has unlimited number of elements. A finite set has finite, countable number of elements. An empty set or null set or void set has no elements. It is written as { } or .

*  The number of (different) elements in a set is called its cardinal number. Thus the cardinal number of a null set is zero, whereas cardinal number of an infinite set is not defined. Cardinal number of a singleton set is 1.

 * Two sets are called equal (written as A B) if they have the same elements. Two finite sets are called equivalent if they have the same number of elements. Thus A B if n(A) = n(B).

* Two sets are called disjoint if they have no elements in common.

*  Two sets are called overlapping if they have some elements in common.

*    A set that contains all the elements under consideration in a given problem is called universal set. It is written as U or .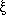

*   Set A is called subset of B if every element of A is also an element of B. We write it as AB (read as "A is a subset of B" or "A is contained in B"). In such a case, we say BA ("B is a superset of A" or "B contains A").

*    Set A is called a proper subset of set B if every element of A is element of B but there exists at least one element of B which is not an element of A.

Posted in: