In mathematics, a matrix (plural matrices) is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. The individual items in a matrix are called its elements or entries. An example of a matrix with 2 rows and 3 columns is
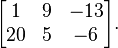
Matrices of the same size can be added or subtracted element by element. The rule for matrix multiplication is more complicated, and two matrices can be multiplied only when the number of columns in the first equals the number of rows in the second.
A major application of matrices is to represent linear transformations, that is, generalizations of linear functions such as f(x) = 4x. For example, the rotation of vectors in three dimensional space is a linear transformation. If R is a rotation matrix and v is a column vector (a matrix with only one column) describing the position of a point in space, the product Rv is a column vector describing the position of that point after a rotation. The product of two matrices is a matrix that represents the composition of two linear transformations.
Another application of matrices is in the solution of a system of linear equations. If the matrix is square, it is possible to deduce some of its properties by computing its determinant. For example, a square matrix has an inverse if and only if its determinant is not zero. Eigenvalues and eigenvectors provide insight into the geometry of linear transformations.
Matrices find applications in most scientific fields. In physics, matrices are used to study electrical circuits, optics, and quantum mechanics. In computer graphics, matrices are used to project a 3-dimensional image onto a 2-dimensional screen, and to create realistic-seeming motion. Matrix calculus generalizes classical analytical notions such as derivatives and exponentials to higher dimensions.
A major branch of numerical analysis is devoted to the development of efficient algorithms for matrix computations, a subject that is centuries old and is today an expanding area of research. Matrix decomposition methods simplify computations, both theoretically and practically. Algorithms that are tailored to the structure of particular matrix structures, e.g. sparse matrices and near-diagonal matrices, expedite computations in finite element method and other computations. Infinite matrices occur in planetary theory and in atomic theory. A simple example is the matrix representing the derivative operator, which acts on the Taylor series of a function.
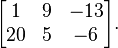
Matrices of the same size can be added or subtracted element by element. The rule for matrix multiplication is more complicated, and two matrices can be multiplied only when the number of columns in the first equals the number of rows in the second.
A major application of matrices is to represent linear transformations, that is, generalizations of linear functions such as f(x) = 4x. For example, the rotation of vectors in three dimensional space is a linear transformation. If R is a rotation matrix and v is a column vector (a matrix with only one column) describing the position of a point in space, the product Rv is a column vector describing the position of that point after a rotation. The product of two matrices is a matrix that represents the composition of two linear transformations.
Another application of matrices is in the solution of a system of linear equations. If the matrix is square, it is possible to deduce some of its properties by computing its determinant. For example, a square matrix has an inverse if and only if its determinant is not zero. Eigenvalues and eigenvectors provide insight into the geometry of linear transformations.
Matrices find applications in most scientific fields. In physics, matrices are used to study electrical circuits, optics, and quantum mechanics. In computer graphics, matrices are used to project a 3-dimensional image onto a 2-dimensional screen, and to create realistic-seeming motion. Matrix calculus generalizes classical analytical notions such as derivatives and exponentials to higher dimensions.
A major branch of numerical analysis is devoted to the development of efficient algorithms for matrix computations, a subject that is centuries old and is today an expanding area of research. Matrix decomposition methods simplify computations, both theoretically and practically. Algorithms that are tailored to the structure of particular matrix structures, e.g. sparse matrices and near-diagonal matrices, expedite computations in finite element method and other computations. Infinite matrices occur in planetary theory and in atomic theory. A simple example is the matrix representing the derivative operator, which acts on the Taylor series of a function.






 ,
,  , see
, see 



